研究報
Research Expectations
理工学部 研究ガイド2024
兼子 裕大 KANEKO Yuki
数理・物理コース 講師
早稲田大学大学院基幹理工学研究科数学応用数理専攻博士課程修了。博士(理学)。日本学術振興会特別研究員DC2・PD、早稲田大学基幹理工学部数学科助教・講師、日本女子大学理学部数物科学科助教を経て、現職。「解析学Ⅰ・Ⅱ」「数理統計学Ⅰ・Ⅱ」などを担当。
自然現象から社会の動向まで“拡散”をテーマに紐解く
水の中に垂らされた一滴のインク、動物の生息分布、人から人へと伝わっていく噂話……。まったくの無関係に思われるこれらの事象について、共通するキーワードがある。それが“拡散”だ。インクは広がって透明な水を濁し、噂話はメディアなどを介しながら社会に拡散される。こうした拡散現象に対し、非線形偏微分方程式の一種である反応拡散方程式を用いることで解を導き出しているのが数理・物理コースの兼子裕大先生。拡散は自然現象や社会現象などあらゆるところに存在し、数理的な解析を通じてその謎や仕組みを解明できるのだと話す。
「いずれの拡散現象についても、時間の経過に伴って広がり、やがて収束するというプロセスは同じです。そこに外部要因が加わることによって、拡散が増進したり減退したりする。例えば、人口の推移を方程式で表す際には、出生率や政策による影響を考慮しなくてはなりません。現象ごとの特徴を数式に落とし込むことによって、より精度の高い数理モデルの確立が実現可能となるのです」
数学を探究することで自然の偉大さを知る
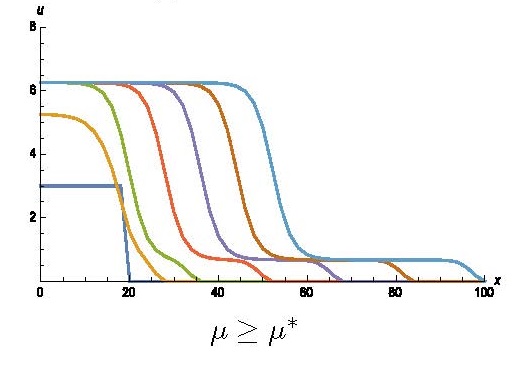
兼子先生が関心を寄せているテーマのひとつに、外来生物の拡散がある。例えば1900年代の初め、毛皮の採取を目的として欧州に持ち込まれたマスクラット。しかし、現地の生態系に侵入した数匹の個体が数を増やし、農作物を食い荒らすといった深刻な被害をもたらした。「初期の研究では、マスクラットが生息する領域の面積を分析していました。近年、生息分布や生息領域の境界を明示するための数理モデルの研究が進められており、私もその課題に取り組んでいます。実際にシミュレーションしてみると、思いもしなかった動きを見せることがあります。そうした未知の現象について、数式で理論的な裏付けができた瞬間にはやりがいを覚えますね」
高校生のころ、「未来を予測する微分方程式」と題された科学雑誌に感銘を受けたと語る兼子先生。自らも世の中の謎を解き明かしたいと進んだ現在の道で、大きな壁に直面する場面もあるという。
「拡散現象について研究していると、人は自然には敵わないのだと改めて実感します。複雑な方程式を組み立てることでようやく説明できたメカニズムが、自然界では当然のように営まれているのですから。しかし、数学がなければそうした偉大さに気づくことすらできません。拡散現象は世界のいたるところにありふれているからこそ、研究する意義のあるテーマなのだと思います」
